Ciao, mi chiamo Drilon e sono un programmatore con la passione per la finanza personale, in questo articolo proverò a fare una previsione delle azioni di Facebook utilizzando Machine Learning.
Il programma leggerà i dati di borsa su Facebook (FB) e farà una previsione del prezzo in base al giorno.
È estremamente difficile provare a prevedere la direzione del mercato azionario o del prezzo delle azioni, ma in questo articolo ci proverò. Anche le persone con una buona conoscenza delle statistiche e delle probabilità hanno difficoltà a farlo.
Una Support Vector Regression (SVR) è un tipo di Support Vector Machine ed è un tipo di algoritmo di apprendimento supervisionato che analizza i dati per l’analisi di regressione .
Inizia la programmazione
La prima cosa che mi piace fare prima di scrivere una singola riga di codice è inserire una descrizione nei commenti di ciò che fa il codice. In questo modo posso rivedere il mio codice e sapere esattamente cosa fa.
#Descrizione: questo programma prevede il prezzo delle azioni FB per un giorno specifico
# utilizzando l'algoritmo di Machine Learning chiamato
# Modello di regressione vettoriale di supporto (SVR)
Ora importa i pacchetti per semplificare la scrittura del programma.
#importa i pacchetti
from sklearn.svm import SVR
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
plt.style.use('fivethirtyeight')
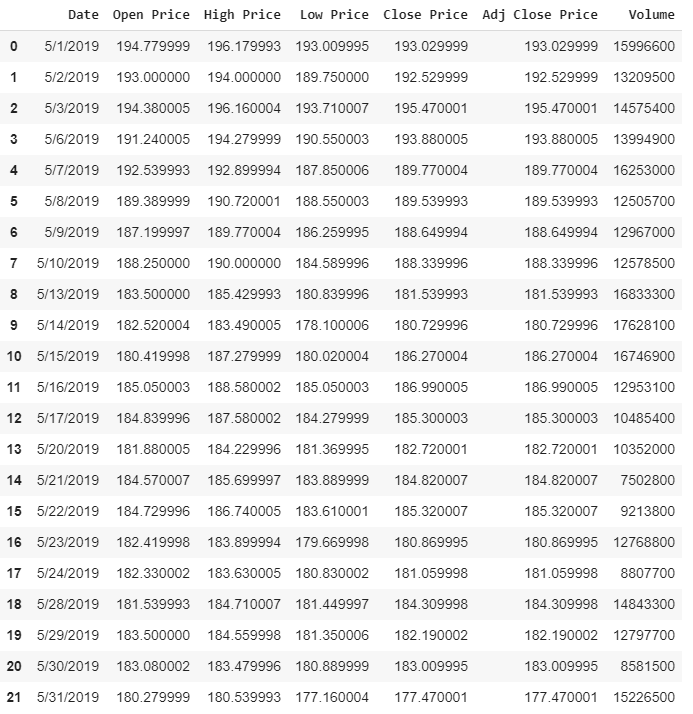
Successivamente caricherò i dati sulle azioni di Facebook (FB) che ho ricevuto da finance.yahoo.com in una variabile chiamata “df”, abbreviazione di data frame.
NOTA: Questi sono i dati di Yahoo per gli ultimi 30 giorni, dal 5–1–2019 al 5–31–2019.
Ricorda che il mercato è aperto solo nei giorni feriali.
#Carica i dati
df = pd.read_csv('FB_Stock.csv')
df
Ottieni il numero di righe e colonne nel set di dati per vedere il conteggio di ciascuna. Ci sono 22 righe e 7 colonne di dati.
#Ottiene il numero di righe e colonne nel set di dati
df.shape
Stampa l’ultima riga di dati (questi saranno i dati su cui testeremo). Si noti che la data è 05–31–2019, quindi il giorno è 31. Questo sarà l’input del modello per prevedere il prezzo di chiusura rettificato che è $ 177,470001.
#Stampa l'ultima riga di dati prezzo_effettivo = df.tail(1) prezzo_effettivo

Creare le variabili che verranno utilizzate come insiemi di dati indipendenti e dipendenti impostandole come elenchi vuoti.
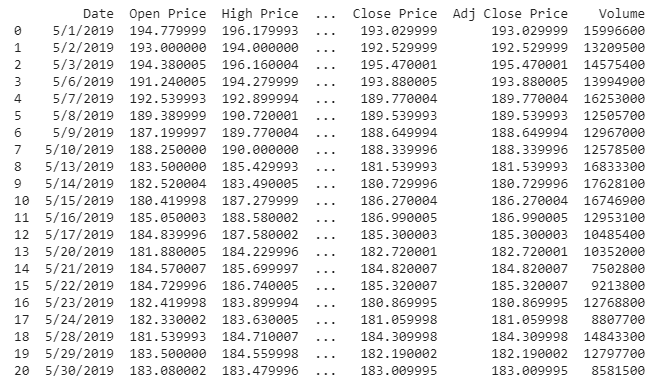
Ricrea il frame di dati recuperando tutti i dati tranne l’ultima riga che userò per testare i modelli in seguito e memorizza i nuovi dati con l’ultima riga mancante in “df”. Quindi stampare il nuovo conteggio di righe e colonne per il nuovo set di dati.
#Ottieni tutti i dati tranne l'ultima riga df = df.head(len(df)-1) print(df) print(df.shape)
#Crea le liste / Set di dati X e y days = list() adj_close_prices = list()
Ottieni tutte le righe dalla colonna Data, memorizzale in una variabile chiamata “df_days” e ottieni tutte le righe dalla colonna Adj Close Price e memorizza i dati in una variabile chiamata “df_adj_close_price”.
df_days = df.loc[:,'Date']
df_adj_close = df.loc[:,'Adj Close Price']
Crea il set di dati indipendente ‘X’ e memorizza i dati nella variabile ‘days’.
Crea il set di dati dipendente “y” e archivia i dati nella variabile “adj_close_prices”.
Entrambi possono essere eseguiti aggiungendo i dati a ciascuna delle liste.
NOTA: per il set di dati indipendente vogliamo solo il giorno dalla data, quindi utilizzo la funzione split per ottenere solo il giorno e trasmetterlo a un numero intero mentre aggiungo i dati all’elenco.
#Crea il set di dati indipendente 'X' come giorni
for giorno in df_days:
days.append( [int(day.split('/')[1]) ] )
#Crea il set di dati dipendente 'y' come prezzi
for adj_close_price in df_adj_close:
adj_close_prices.append(float(adj_close_price))
Guarda e guarda quali giorni sono stati registrati nel set di dati.
stampa (days)

Successivamente, creerò e addestrerò i 3 diversi modelli di Support Vector Regression (SVR) con tre diversi kernel per vedere quale funziona meglio.
#Crea e addestra un modello SVR usando un kernel lineare lin_svr = SVR(kernel='linear', C=1000.0) lin_svr.fit(days,adj_close_prices) #Crea e addestra un modello SVR utilizzando un kernel polinomiale poly_svr = SVR(kernel='poly', C=1000.0, degree=2) poly_svr.fit(days, adj_close_prices) #Crea e addestra un modello SVR utilizzando un kernel RBF rbf_svr = SVR(kernel='rbf', C=1000.0, gamma=0.15) rbf_svr.fit(days, adj_close_prices)
Ultimo ma non meno importante, traccerò i modelli su un grafico per vedere quale ha il miglior adattamento e restituirà la previsione del giorno.
#Traccia i modelli su un grafico per vedere quale ha il miglior fit
plt.figure(figsize=(16,8))
plt.scatter(days, adj_close_prices, color = 'black', label='Data')
plt.plot( days, rbf_svr.predict(days), color = 'green', label='RBF Model')
plt.plot(days, poly_svr.predict(days), color = 'orange', label='Polynomial Model')
plt. plot(days, lin_svr.predict(days), color = 'blue', label='Linear Model')
plt.xlabel('Days')
plt.ylabel('Adj Close Price')
plt.title('Support Vector Regression ')
plt.legend()
plt.show()
Il miglior modello dal grafico sottostante sembra essere l’ RBF che è un modello di regressione del vettore di supporto che utilizza un kernel chiamato funzione di base radiale. Tuttavia questo grafico può essere fuorviante.
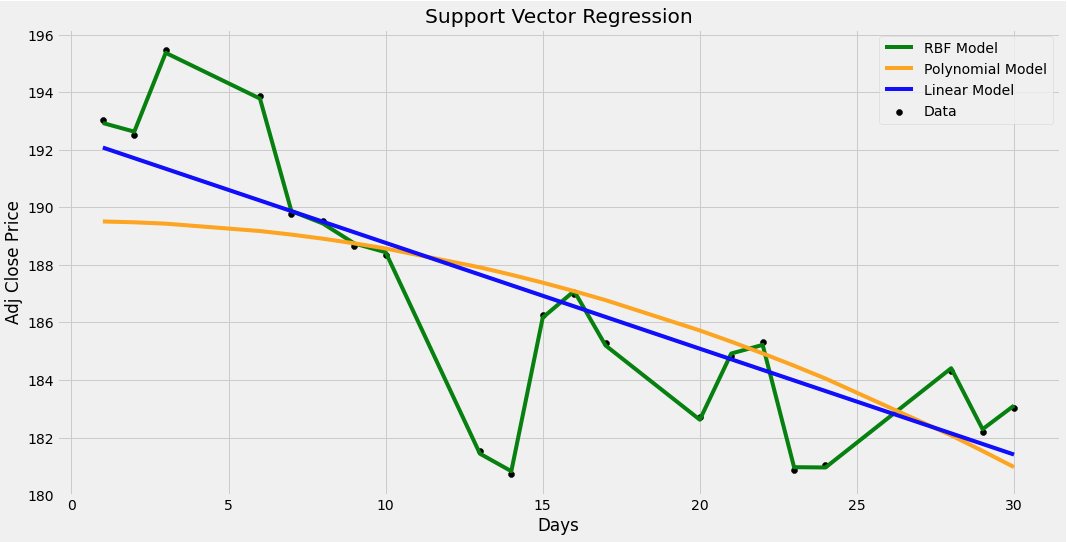
Ora posso iniziare a fare la mia previsione dei prezzi su FB. Ricordando l’ultima riga di dati che è stata lasciata fuori dal set di dati originale, la data era 05–31–2019, quindi il giorno è 31. Questo sarà l’input per i modelli per prevedere il prezzo di chiusura rettificato che è $ 177,470001 .
Quindi ora prevedo il prezzo assegnando ai modelli un valore di 31.
day = [[31]]
print('Il prezzo previsto da SVR RBF:',rbf_svr.predict(day))
print('Il prezzo previsto da SVR lineare',lin_svr.predict(day))
print('Il prezzo previsto da SVR polinomiale ',poly_svr.predict(giorno))

Il modello SVR polinomiale ha previsto che il prezzo per il giorno 31 fosse di $ 180,39533267 , che è abbastanza vicino al prezzo effettivo di $ 177,470001 . In questo caso il modello migliore sembra essere il polinomio SVR. Ecco fatto, hai finito di creare il tuo programma SVR per prevedere le azioni FB!
Se sei interessato a leggere di più sull’apprendimento automatico per iniziare immediatamente con problemi ed esempi, ti consiglio vivamente di dare un’occhiata all’Apprendimento automatico pratico con Scikit-Learn e TensorFlow: concetti, strumenti e tecniche per costruire sistemi intelligenti .
È un ottimo libro per iniziare a imparare come scrivere programmi di apprendimento automatico e comprendere i concetti di apprendimento automatico.

Se hai dubbi o domande fammele pure su Telegram: https://t.me/+0xQYD3WKIAA5Mjg8
Instagram: https://www.instagram.com/investoinvestigando.it/
Dai un’occhiata anche al resto: https://www.investoinvestigando.it




